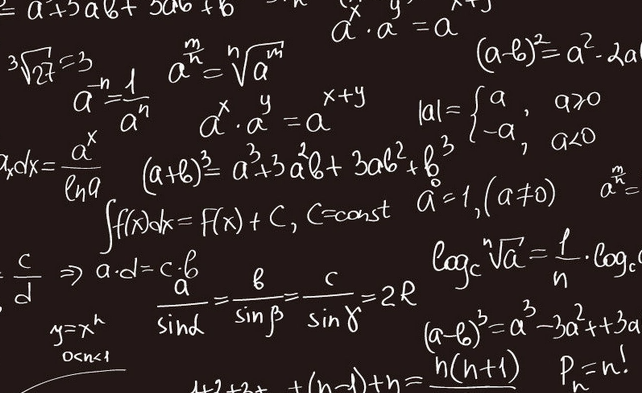数学事什么学科数学本质是看到什么想到什么吗

溺于你心2023-03-23 12:26:242451

数学是研究什么的科学？数学是什么？什么是数学？什么是数学？数学是一门怎么样的科目？什么叫做什么叫做数学？

本文导航

数学本质是看到什么想到什么吗
数学到底包含哪些
数学什么叫做组成
数学里面的定义是什么
数学包括了哪一科
数学的基础是什么

数学本质是看到什么想到什么吗

什么是数学？有人说：“数学，不就是数的学问吗？”

这样的说法可不对。因为数学不光研究“数”，也研究“形”，大家都很熟悉的三角形、正方形，也都是数学研究的对象。

历史上，关于什么是数学的说法更是五花八门。有人说，数学就是关联；也有人说，数学就是逻辑，“逻辑是数学的青年时代，数学是逻辑的壮年时代。”

那么，究竟什么是数学呢？

伟大的革命导师恩格斯，站在辩证唯物主义的理论高度，通过深刻分析数学的起源和本质，精辟地作出了一系列科学的论断。恩格斯指出：“数学是数量的科学”，“纯数学的对象是现实世界的空间形式和数量关系”。根据恩格斯的观点，较确切的说法就是：数学——研究现实世界的数量关系和空间形式的科学。

数学可以分成两大类，一类叫纯粹数学，一类叫应用数学。

纯粹数学也叫基础数学，专门研究数学本身的内部规律。中小学课本里介绍的代数、几何、微积分、概率论知识，都属于纯粹数学。纯粹数学的一个显著特点，就是暂时撇开具体内容，以纯粹形式研究事物的数量关系和空间形式。例如研究梯形的面积计算公式，至于它是梯形稻田的面积，还是梯形机械零件的面积，都无关紧要，大家关心的只是蕴含在这种几何图形中的数量关系。

应用数学则是一个庞大的系统，有人说，它是我们的全部知识中，凡是能用数学语言来表示的那一部分。应用数学着限于说明自然现象，解决实际问题，是纯粹数学与科学技术之间的桥梁。大家常说现在是信息社会，专门研究信息的“信息论”，就是应用数学中一门重要的分支学科，数学有3个最显著的特征。

高度的抽象性是数学的显著特征之一。数学理论都算有非常抽象的形式，这种抽象是经过一系列的阶段形成的，所以大大超过了自然科学中的一般抽象，而且不仅概念是抽象的，连数学方法本身也是抽象的。例如，物理学家可以通过实验来证明自己的理论，而数学家则不能用实验的方法来证明定理，非得用逻辑推理和计算不可。现在，连数学中过去被认为是比较“直观”的几何学，也在朝着抽象的方向发展。根据公理化思想，几何图形不再是必须知道的内容，它是圆的也好，方的也好，都无关紧要，甚至用桌子、椅子和啤酒杯去代替点、线、面也未尝不可，只要它们满足结合关系、顺序关系、合同关系，具备有相容性、独立性和完备性，就能够构成一门几何学。

体系的严谨性是数学的另一个显著特征。数学思维的正确性表现在逻辑的严谨性上。早在2000多年前，数学家就从几个最基本的结论出发，运用逻辑推理的方法，将丰富的几何学知识整理成一门严密系统的理论，它像一根精美的逻辑链条，每一个环节都衔接得丝丝入扣。所以，数学一直被誉为是“精确科学的典范”。

广泛的应用性也是数学的一个显著特征。宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。20世纪里，随着应用数学分支的大量涌现，数学已经渗透到几乎所有的科学部门。不仅物理学、化学等学科仍在广泛地享用数学的成果，连过去很少使用数学的生物学、语言学、历史学等等，也与数学结合形成了内容丰富的生物数学、数理经济学、数学心理学、数理语言学、数学历史学等边缘学科。

各门科学的“数学化”，是现代科学发展的一大趋势。

数学到底包含哪些

数学（mathematics或maths，来自希腊语，“máthēma”；经常被缩写为“math”），是研究数量、结构、变化、空间以及信息等概念的一门学科，从某种角度看属于形式科学的一种。数学家和哲学家对数学的确切范围和定义有一系列的看法。

而在人类历史发展和社会生活中，数学也发挥着不可替代的作用，也是学习和研究现代科学技术必不可少的基本工具。

中文名

数学

外文名

Mathematics（简称Maths或Math）

学科分类

一级学科

数学什么叫做组成

数学里面的定义是什么

1+1=2

数学是任何事物的可量度属性，即数学属性是事物最基本的属性。可量度属性的存在与参数无关，但其结果却取决于参数的选择。例如：时间，不管用天、月还是用年、时分秒来量度，它的可量度属性永远存在，但准确性与这些参数有关。数学是研究数量、结构、变化以及空间模型等概念的一门学科。透过抽象化和逻辑推理的使用，由计数、计算、量度和对物体形状及运动的观察中产生。数学家们拓展这些概念，为了公式化新的猜想以及从合适选定的公理及定义中建立起严谨推导出的真理。数学是研究现实世界中数量关系和空间形式的科学。简单地说，是研究数和形的科学。由于生活和劳动上的需求，即使是最原始的民族，也知道简单的计数，并由用手指或实物计数发展到用数字计数。

数学包括了哪一科

数学：是研究数量、结构、变化、空间以及信息等概念的一门学科。数学是研究现实世界空间形式和数量关系的一门科学。分为初等数学和高等数学。它在科学发展和现代生活生产中的应用非常广泛，是学习和研究现代科学技术必不可少的基本工具。

数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段，可以应用于现实世界的任何问题，所有的数学对象本质上都是人为定义的。从这个意义上，数学属于形式科学，而不是自然科学。不同的数学家和哲学家对数学的确切范围和定义有一系列的看法。

在人类历史发展和社会生活中，数学发挥着不可替代的作用，同时也是学习和研究现代科学技术必不可少的基本工具。

结构

许多诸如数、函数、几何等的数学对象反应出了定义在其中连续运算或关系的内部结构。数学就研究这些结构的性质，例如：数论研究整数在算数运算下如何表示。

此外，不同结构却有着相似的性质的事情时常发生，这使得通过进一步的抽象，然后通过对一类结构用公理描述他们的状态变得可能，需要研究的就是在所有的结构里找出满足这些公理的结构。因此，我们可以学习群、环、域和其他的抽象系统。

把这些研究（通过由代数运算定义的结构）可以组成抽象代数的领域。由于抽象代数具有极大的通用性，它时常可以被应用于一些似乎不相关的问题，例如一些古老的尺规作图的问题终于使用了伽罗瓦理论解决了，它涉及到域论和群论。

代数理论的另外一个例子是线性代数，它对其元素具有数量和方向性的向量空间做出了一般性的研究。这些现象表明了原来被认为不相关的几何和代数实际上具有强力的相关性。组合数学研究列举满足给定结构的数对象的方法。

以上内容参考;;百度百科 ;数学

数学的基础是什么

数学是研究现实世界中数量关系和空间形式的科学。简单地说，是研究数和形的科学。由于生活和劳动上的需求，即使是最原始的民族，也知道简单的计数，并由用手指或实物计数发展到用数字计数。　　基础数学的知识与运用总是个人与团体生活中不可或缺的一块。其基本概念的精炼早在古埃及、美索不达米亚及古印度内的古代数学文本内便可观见。从那时开始，其发展便持续不断地有小幅的进展，直至16世纪的文艺复兴时期，因著和新科学发现相作用而生成的数学革新导致了知识的加速，直至今日。　　今日，数学被使用在世界上不同的领域上，包括科学、工程、医学和经济学等。数学对这些领域的应用通常被称为应用数学，有时亦会激起新的数学发现，并导致全新学科的发展。数学家亦研究没有任何实际应用价值的纯数学，即使其应用常会在之后被发现。　　创立于二十世纪三十年代的法国的布尔巴基学派认为：数学，至少纯粹数学，是研究抽象结构的理论。结构，就是以初始概念和公理出发的演绎系统。布学派认为，有三种基本的抽象结构：代数结构（群，环，域……），序结构（偏序，全序……），拓扑结构（邻域，极限，连通性，维数……）。数学分支　　1.算术　　2.初等代数　　3.高等代数　　4. 数论　　5.欧式几何　　6.非欧式几何　　7.解析几何　　8.微分几何　　9.代数几何　　10.射影几何学　　11.拓扑几何学　　12.拓扑学　　13.分形几何　　14.微积分学　　15. 实变函数论　　16.概率和数量统计　　17.复变函数论　　18.泛函分析　　19.偏微分方程　　20.常微分方程　　21.数理逻辑　　22.模糊数学　　23.运筹学　　24.计算数学　　25.突变理论　　26.数学物理学